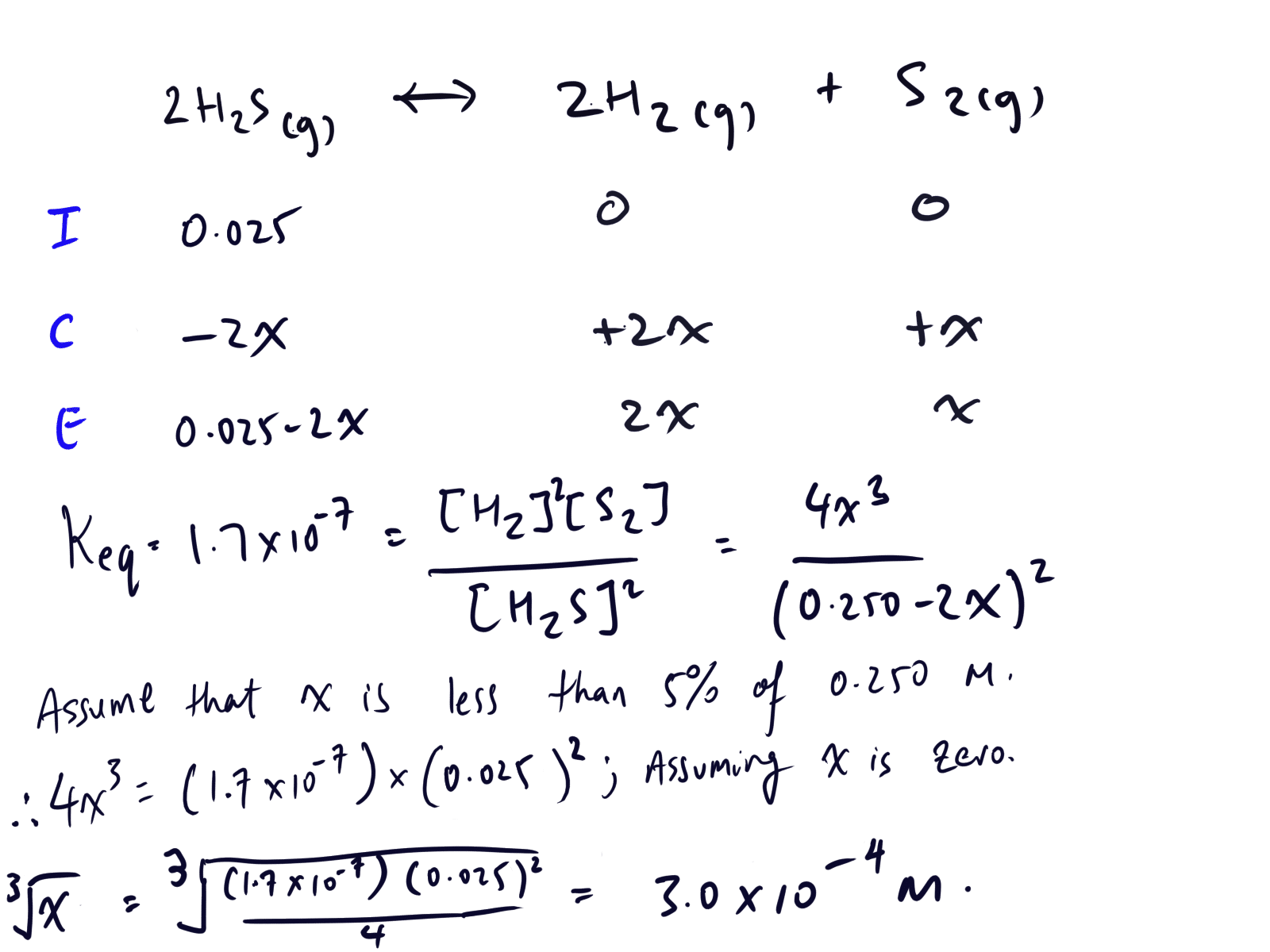HSC Chemistry Notes

Module 5 / Inquiry Question 3

Overview of Week 3 Inquiry Question – Describe position of equilibrium and what does equilibrium constant represent?

Learning Objective #1 – Deduce the equilibrium expression for homogeneous reactions occurring in a solution

Learning Objective #2 – Perform calculations to determine concentration of species, Keq value and direction which equilibrium position will shift.

Learning Objective #3 – Qualitatively analyse the effect of temperature on the value of Keq

Learning Objective #4 – Explain how Keq can be used to explain the dissociation of acids and bases (heterogeneous reactions briefly mentioned here)

Learning Objective #5 – Explain how Keq can be used to explain the dissociation of ionic solutions (heterogeneous reactions briefly mentioned here)

Learning Objective #6 – Calculate the equilibrium constant for iron (III) thiocyanate equilibrium

NEW HSC Syllabus Chemistry Syllabus Video – Equilibrium Constant

Week 3 Homework Problem Set

Week 3 Curveball Questions (Moving from Band 5 to Band 6!)

Week 3 Extension Questions

Solutions to Week 3 Questions 

Overview of Inquiry Question 3

In the prior weeks, we have explored what equilibrium reactions are, the factors that affects an equilibrium’s position, how we can use Le Chatelier’s Principle to predict which direction an equilibrium will shift and many other smaller things under those concepts.

In this week’s notes, we will look into the concept of equilibrium constant in homogeneous reactions (as well as heterogeneous reactions).

We will have a look at how there are many types of equilibrium constants and which we will use depending on the type of equilibrium reaction we are dealing with.

Also, we will explore how temperature affects equilibrium constant. Yes, temperature is the only factor.

After that, we will explore how equilibrium constant will allow us to determine the concentration of species that is involved in an equilibrium reaction using the equilibrium constant formula and ICE table. By understanding the concentration of species (reactants and products), we can understand how the equilibrium position of system looks like at equilibrium, i.e. the extent of which the position is lying on the left or right.

We will have a look at how the equilibrium constant will allow us to predict the relative solubilities between ionic compounds as well as what defines a strong or weak acid and a strong or weak base.

Learning Objective #1 - Deduce the equilibrium expression (in terms of Keq) for homogeneous reactions occurring in a solution

Alright, let’s start by understanding what homogeneous reactions mean here. 

An equilibrium reaction is deemed homogeneous if all species involved in the equilibrium are in the SAME state of matter: solid, liquid, aqueous or gas. 

Therefore, if a chemical equilibrium can be called heterogeneous if it has one or more participating species with a different state of matter compared to the rest. 

• For example, the reaction involving a solid and liquid would be called a heterogeneous reaction, or, a heterogeneous equilibrium if they’re operating in an equilibrium.

Back to the topic of homogeneous equilibria that we’re concerned about, let’s use the following equilibrium to illustrate how we can construct a formula in computing the equilibrium expression in terms of Keq as per learning objective!

N2(g) + 3H2(g) <-> 2NH3(g)

You should be familiar with the above chemical equilibrium reaction, the Haber Process, used to produce ammonia as we have used it a few times in the last two weeks’ notes. So, we might as well use it again. 

P.S: Yes, if you noticed the learning objective requires us to understand Keq for solutions and not gaseous equilibrium reactions. We will go over an example for aqueous equilibrium towards the end of this learning objective. You will see that the theory is similar. 

As you can see, the state of matter for all species involved in the Haber Process are the same. They are all gases! The Haber Process is therefore a homogeneous equilibrium! 

The equilibrium constant (Keq) of the Haber Process can be written as and computed as: 

Can you spot the relationships between the equilibrium reaction and the equilibrium constant formula?

The substances on the right hand side of the equilibrium reaction is the numerator and the substances on the left hand side of the equilibrium reaction make up the denominator of the equilibrium constant formula! That is, the products became the numerator and vice versa for the reactants. 

There are few more things about the equilibrium constant that requires your attention:

When we are dealing with the concentration of species involved in an equilibrium, the units of the species involved, regardless if they are in the numerator or denominator, must in moles per litre (mol/L or M). 

Therefore, if we are dealing with the concentration of reactants & products species involved in an equilibrium reaction, we can re-write Keq as Kc. 

However, sometimes the question may be of gas equilibrium and, instead of providing us with the concentration of the gases, the question may opt to provide us with each of the gases’ pressure (i.e. partial pressure) which can be used to find equilibrium constant of the gas equilibrium.

In that case, we need to insert each of the gases’ partial pressure to calculate the equilibrium constant but the formula is the same, just the units are different. Recall that pressure units can be expressed in kPa or atm whereas concentration is M. 

When pressure units are given for each gas species to calculate equilibrium constant, we can re-write Keq as Kp. 

Back to exploring Keq in the form of Kc, a second thing about the equilibrium constant expression that we provided as an example earlier using the Haber Process reaction is that the concentrations of the species in the numerator and denominators are raised to a certain power! 

This power is governed by each species’s coefficients in the equilibrium equation: N2 + 3H2 <-> 2NH3. 

Hence, nitrogen is raised to the power of 1. Hydrogen is raised to the power of 3 and, lastly, ammonia is raised to the power of 2. 

NOTE: In the exam, if the coefficient of a participating species is 1 (such as nitrogen in this case), there is NO need to write it as a power, just like in mole coefficients in chemical equations. I only wrote “1” as the power for nitrogen in the diagram for illustrative purposes to get the concept through to you.

NOTE: Sometimes you may find yourself in a situation where a fraction is used as an coefficient for a species in order to balance equation. For example: 2A(g) + 1/2 B2(g) <-> A2B(g) 

In this case, B will be raised to the power of 1/2 in your equilibrium constant expression. 

• According to algebraic rules for fractional powers, a number (in this case, the number is concentration of B in expressed in mol/L), raised the power of 1/2 is equivalent to the square root of that number (concentration of B). So, for this example, raising B to the power of 1/2 would be equivalent to taking the square root of the concentration of B (mol/L).

• If you don’t exactly understand this right now, don’t be afraid. We will have questions for you to attempt at the end of this week’s notes with detail solutions provided!

You may see this as a multiple choice option in HSC Chemistry MCQ exams. So don’t get thrown off by some algebraic tricks!

• If you given the option of writing out a chemical reaction yourself (and NOT written and given to you on paper), it is BEST for you to write the coefficient of each species at their lowest whole number coefficient and avoid fractions as it is the standard convention.

NOTE: It is important to note that, in HSC Chemistry, the equilibrium constant values can be reported without units. This is because we use an assumption that K⁰ = K which if often used at university level too. 

• In practice, this assumption is wrong and, if you wish to understand why this assumption is used, feel free to join the discord community as we have a comprehensive PDF explaining this.

• Anyways, for HSC purpose, just know that equilibrium constant is unitless.

Another point about equilibrium constants is that different equilibrium chemical equilibrium reactions have their own equilibrium value. Therefore, two different equilibrium reactions will have different equilibrium values.

Next, you need to know that there are different types of equilibrium constants (Keq). 

We have briefly touched on Kc and Kp. There are others which are Ka and Kb and Ksp which we will briefly explore them later in this week’s notes.

For now, let’s continue swimming deeper into Kc and Kp.

So, we have already said that Kc is used when you are dealing with species in an equilibrium and you are provided their concentration to find the equilibrium constant for the reaction. This can be the concentration of gases or aqueous ions in solution. 

On the other hand, Kp is used to determine the equilibrium constants involving gases at equilibrium. When given their partial pressures, you will need to use Kp to find the equilibrium constant of the reaction. Partial pressure of a gas is essentially the pressure that the gas exerts onto the system. The sum of all of the gases’ partial pressure is equal the total pressure of the system which you have learnt in HSC Preliminary Chemistry.

The equilibrium constant formulae are the same but the units of each species are different – Kc deals with concentration and Kp deals with partial pressure of gases. 

Recall from Week 1 Notes that equilibrium reactions have forward and reverse reactions. What happens if we want to find out equilibrium constant of the reverse reaction? 

For example, we found the equilibrium constant of forward reaction of Haber process previously, but what if we want to find out the equilibrium constant of reverse reaction, i.e. ammonia being converted into hydrogen and nitrogen gases. 

To do this, simply calculate the reciprocal of the equilibrium constant of the forward reaction, i.e. 1/Keq. 

Recall in preliminary chemistry when you dealt with Hess Law, you had to manipulate several chemical equations to find out enthalpy of a given (different) chemical reaction. 

Well, if you combine equations together in other to form a new, overall chemical equation, you need to MULTIPLY each of the combined equations’ equilibrium constants to find the Keq of the new, overall (combined) chemical equation. 

• Don’t be afraid. There will be some exercises on manipulating equilibrium constants with detail solutions in this week’s homework set.

Lastly,  equilibrium constant is essentially a ratio between product and reactant species in some measurement units (e.g. concentration, partial pressure, etc).

• Therefore, if Keq is greater than 1, it would mean that, at equilibrium, there will be more products than reactants in terms of concentration.

• Contrastingly, if Keq is less than 1, it would mean that, at equilibrium, there will be more reactants than products.

As promised, to finish off this learning objective, let’s explore equilibrium constant expression for a homogeneous equilibrium reaction in solution! 

We so far only touched on gas equilibrium, N2(g) + 3H2(g) <-> 2NH3(g) but learning objective wants us to construct Keq for homogeneous solutions (aq).

Suppose we have the following equilibrium reaction:

A(aq) + B(aq) <-> 2C(aq)

Well, Keq (or Kc) will be simply = [C]2/ [A][B]

So what is the definition equilibrium constant after all this? 

Well, it is the ratio between the concentration of species (ratio of product to reactant) at equilibrium! 

Hence, by working out or using Keq, you can find out the exact concentrations (amount) of each species at equilibrium involved in the equilibrium reaction! 

And from this you will understand the extent of which the equilibrium position is leaning on the left or right side of the chemical equation, i.e. if the reaction is reactant-favoured or product-favoured.

NOTE: By the way, the values for each species (e.g. concentration, partial pressure, etc) that you plug into the equilibrium constant formula are their values AT EQUILIBRIUM and NOT their initial or current values. 

• You will have a better understanding of this in the next learning objective where we touch on the formula for reaction quotient in which we use the initial or current values of the species involved in the equilibrium reaction.

Learning Objective #2 - Perform calculations to find the value of Keq and the concentrations of substances within an equilibrium system, and use these values to make predictions on the direction in which a reaction may proceed

Alright! Let’s try find out the equilibrium concentration of the species involved in a chemical equilibrium by using Keq! All abroad the materialistic train! Choo Choo!

So, as per learning objective, we want to find the concentration of substances AT EQUILIBRIUM.

Usually, in exam questions, we are going to be asked to find the concentration of substances at equilibrium when given their current or initial concentrations.

Respectively, initial concentration means the concentration of species at the start of the equilibrium reaction when there is no products, only reactants. Current concentration may often to concentration of species at a certain stage in the equilibrium reaction (usually when the system hasn’t reached equilibrium yet). 

Using such information, we can find Keq and use Keq to find the concentration of species AT EQUILIBRIUM. How? Well, we use the ICE table as you will see very soon.

Before we can start using the ICE table, let’s start up a scenario with some data values for us to work with.

Let’s suppose we have this equilibrium: H2O(g) + CO(g) <-> H2(g) + CO2(g)

Suppose the initial concentration of steam and carbon monoxide are both 0.500 moles per litre (M). The temperature is 1000 Kelvins and they provided us with the equilibrium constant (Kc = 4.3). 

Now let’s say the question wants us find the concentration of all 4 species at equilibrium or when equilibrium has been established/reached.

We can find the solution to this question by constructing an ICE table to help us!

Hence, at equilibrium, the concentrations of each species are shown in red in the above working out. 

For example, from the ICE table, we know that the equilibrium concentration of steam, H2O(g), is 0.500 – x. And by solving for x using Kc = 4.3, alongside using the Keq formula, we found out that x = 0.34 moles per litre. 

Hence, the concentration of steam at equilibrium is equal to 0.500 – 0.34 = 0.16 moles per litre, aka. 0.16M. 

Alright! Well done we now know how to calculate equilibrium concentration of species involved in an equilibrium reaction! 

However, we are still one step away from finishing this learning objective!

Recall that we said earlier that we assume that steam will react with carbon monoxide and form hydrogen and carbon dioxide because at equilibrium there must be both products and reactant present. This means that the equilibrium position must shift to the right in order to form hydrogen and carbon dioxide gases, do you agree?

We can actually verify this! Let’s see how!

We can verify whether the equilibrium position will shift to the right (to produce hydrogen and carbon dioxide) by using the reaction quotient, denoted as Q. The formula for Q is identical in calculating Kc. 

So, Q = [H2][CO2] / [H2O][CO]

In the reaction quotient formula, the concentration of the species that we substitute in are their initial, or more accurately, their current concentrations and NOT the equilibrium concentration of each species like we did in the Keq formula. 

This is because we use the reaction quotient formula to determine whether or not equilibrium has been reached (i.e. when Q value = Keq value). And if not, how will the system will shift its equilibrium position in order to reach equilibrium. 

In our example, we initially assumed that the question conveys that there is no hydrogen and carbon dioxide yet because their initial concentrations were not given.

Hence, Q = [H2][CO2] / [H2O][CO] = (0 x 0) / (0.500 x 0.500) = 0. 

What happens when equilibrium has been reached is that the reaction quotient is equal to the equilibrium constant. 

We have calculated that the reaction quotient (Q) = 0 using the current concentration species given to us in the question. Since 0 is not equal to 4.3 (equilibrium value), it means that reaction quotient is NOT equal to the equilibrium constant for our reaction. 

This means that the reaction is not at equilibrium (as you would’ve expected) when the species have the current concentration as specified in the question. Thus, in order for equilibrium to be established, the reaction quotient, Q, must increase from 0 to 4.3. 

In order for Q to go from zero to 4.3, the numerator must increase so that Q = Keq. 

• That is, the concentration of hydrogen and carbon dioxide must increase such as that:

• Q = Keq = 4.3 = [H2][CO2] / [H2O][CO] = [H2] x [CO2] / (0.500 x 0.500)

• So, [H2] x [CO2] = 4.3 x (0.500 x 0.500) which is greater than zero.

This means that the equilibrium position will shift to the right to create hydrogen and carbon dioxide to establish equilibrium! So our assumption was right! 

• The change in hydrogen and carbon dioxide concentration is positive (+x) as we have written in the ICE table.

Learning Objective #3 - Qualitatively analyse the effect of temperature on the value of Keq

The effect of temperature on the equilibrium constant (Keq) will depend on the type of equilibrium reaction! That is, it will depend on whether the reaction is endothermic or exothermic.

In fact, the concept of how temperature effects the value of Keq have been touched on during last week’s notes! But, let’s see what is going on still.

Let’s first explore endothermic equilibrium reactions (i.e. the forward reaction is endothermic).

Suppose we have the endothermic reaction, A2B(aq) + heat <-> 2A(aq) + B(aq) 

As shown in the equation above, the forward reaction is endothermic. This is because heat is consumed to decompose the compound, A2B. 

So, if there is a temperature increase in the equilibrium system, the system will shift its equilibrium position to the right, in favour of the forward endothermic reaction, to counteract and minimise the increase in temperature. This is because the forward endothermic reaction will consume the excess heat added into the system due to increase in temperature (maybe a scientist heated up the system on a bunsen burner). 

So, as the equilibrium shifts to the right, the concentration of products would increase. This would mean that the equilibrium constant will increase. 

Why? Well, let’s take a look back at the relevant equilibrium constant formula for our reaction:

Keq = [A]2 [B] / [A2B]

As the concentration the products, [A] and [B], or the numerator increases, the fraction (Keq value) will increase. It’s a mathematical relationship! For example, 2/1 is greater than 1/1, i.e. concentration of products increased. This would mean that the equilibrium constant value will increase.

Vice versa, if the temperature decreased for the above endothermic reaction, the equilibrium will shift in favour of the exothermic (reverse) reaction, forming more A2B in order to increase heat and minimise the decrease in temperature. 

This would mean that the denominator of the Keq formula will increase (due to increased concentration of A2B), making the equilibrium constant value smaller. 

Let’s now explore exothermic equilibrium reactions (i.e. the forward reaction is exothermic).

Suppose we have the following exothermic reaction: 2A + B <-> A2B + Heat

When there is an decrease in temperature, the equilibrium position will shift towards the right in favour of the forward exothermic reaction. This is because, by producing more A2B, heat is released as bonds are being formed and this will increase the system’s temperature, minimising the decrease in system’s temperature (maybe the scientist initially cooled the system by putting the system in fridge to lower temperature). 

Therefore, this will increase the numerator of the Keq equation (fraction) and increase the value of Keq.

Vice versa, if the temperature of the system suddenly increased, the equilibrium position will shift towards the left, in favour of the reverse (endothermic) reaction. This is because the endothermic reaction will consume the excess heat and minimise the change in equilibrium temperature. 

This would mean that the concentration reactants will increase. This would increase the denominator value of the Keq equation. This would decrease the value of the Keq.

Learning Objective #4 - Explore the use of Keq for different types of chemical reactions, including
- Dissociation of ionic solutions
- Dissociation of acids and bases

Let’s first have a look at the dissociation of acids.

An (Arrehenius) acid can be defined as a substance that releases one or more hydrogen ion(s) in solution, according to a scientist named Svante Arrhenius. 

For example, the dissociation of the acid, acetic acid (CH3COOH), can be expressed as the following in water:

CH3COOH (aq) <-> H+(aq) + CH3COO–(aq)  [Hydrogen ion (H+) is dissociated from acid molecule in solution]

Recall that at the beginning of this week’s notes, we touched on how there are many types of equilibrium constants. Well, the relevant equilibrium constant for the dissociation of acid is Ka.

Since Ka is an equilibrium constant for the dissociation of acids, it can be calculated like other equilibrium constants:

Ka = [H+] [CH3COO–] / [CH3COOH].

You typically see Ka being referred to the acid dissociation constant. 

Water here is a pure liquid because it is acting as a solvent for the dissociation of acetic acid. This would mean that water will appear on both sides of the chemical equation, both reactant and product side. 

This means that water will cancel each other out in the Ka formula as water appears both on the numerator and denominator. 

So from the Ka expression, you should now see that the value of Ka will increase if the concentration of hydrogen ions (numerator) in solution increased. 

• Strong acids are acids where each acid molecule (e.g. HCl) have their hydrogen ions fully dissociated from the acid molecules in solution, based on Arrhenius’s definition of acids.

• Comparatively, weak acids are acids where their hydrogen ions are not fully dissociated from the acid molecules in solution.

• Acetic acid (CH3COOH) was used in our example is a weak acid so it does not fully dissociate from the acid molecule (CH3COOH) and so an equilibrium is established.

The strength of an acid does not necessarily depend on how many hydrogen ions an acid molecule can potentially release in solution. It depends on the number of hydrogen ions that is actually dissociated in solution over the total amount acid molecules present in solution. 

• Example: An hydrochloric acid (HCl) molecule and an acetic acid acid molecule (CH3COOH) both have the potential to release one hydrogen ion in solution.

• However, in the big picture, if you put 100 HCl in solution, every HCl molecule will release one hydrogen ion in solution, i.e. 100 hydrogen ions. For acetic acid, the amount of hydrogen ions in solution will be fewer as, unlike hydrochloric acid, acetic acid does not have 100% degree of ionisation.

• This is actually Module 6 Content so if you do not understand this right now, it is okay.

• Just recognise how how we expressed the Ka formula for weak acids above. We will formally introduce strong & weak acids in Module 6.

Let’s have a look at the dissociation of bases. The concept very similar to the dissociation of acids.

The (Arrhenius) definition of a base is a substance that releases one or more OH– ions in solution.

For example, the base, NaOH can be expressed in the following manner when dissolved in water:

NaOH (aq) <-> Na+(aq) + OH–(aq)

So, from what we have about equilibrium constant expressions, the base dissociation constant (Kb) can therefore be expressed as the following:

Kb = [Na+] [OH–] / [NaOH]

• As the concentration of hydroxide ions increase, the value of Kb will increase.

• Strong bases are bases where each base molecule (e.g. NaOH) have their hydroxide ions fully dissociated in solution based on Arrhenius’s definition of bases.

• Weak bases are bases where their hydroxide ions are not fully dissociated in solution, thus they establish an equilibrium.

• Again, strong & weak bases will be formally introduced in Module 6 so it’s okay if you don’t understand in terms of degree of dissociation.

• So, for now just understand how we arrived to the Kb equilibrium constant expression shown above.

You will learn more about the application of Ka, Kb and Kw in Module 6! 

• This learning objective really only need you to understand how to write Ka and Kb equilibrium expressions.

• We just introduced ‘degree of ionisation/dissociation’ to give you a taste of Module 6 which we will formally introduced to you soon!

NOTE: The above chemical equations for the dissociation of acids and bases will vary depending if the exam question specifies for Bronsted-Lowry acid or Arrhenius Acid. If the exam question is referring to Arrhenius acid and bases, use the above chemical equations above to express the dissociation of acids and bases.

However, in some exam questions, they may be referring to Bronsted-Lowry acid and bases. In such the scenario, the chemical equations will be different. 

• We will explore how to write equations for Bronsted-Lowry acid and bases in later weeks’ notes.

Dissociation of ionic solutions and equilibrium constant

Suppose we have an ionic compound such as AgCl dissolved in solution, forming an ionic solution. This can be expressed as:

AgCl (s) <-> Ag+ (aq) + Cl– (aq)

We can express the equilibrium constant for the dissociation of AgCl (an ionic compound) as the following:

Ksp = [Ag+] x [Cl–]  ; where Ksp is called the solubility product equilibrium constant. This type of equilibrium constant exists when a sparingly soluble ionic compound interacts with a solution or liquid, allowing it be dissolved. 

• When writing the formula in Ksp questions, the solid (precipitate) is generally insoluble or sparingly soluble, for example, the dissolution of the sparingly soluble AgCl solid in the above example.

• If the solid is completely soluble, an equilibrium will not exist between the solid and the ions as no precipitate will form. You may recall that silver chloride exist as a precipitate in solubility rules table. However, this is inaccurate as some amount of silver chloride can still dissolve in water. To be precise, 0.002 grams of silver chloride will dissolve in 100 grams of water at room temperature.

• So, it is technically more accurate if we call silver chloride sparingly soluble rather than insoluble.

• Because silver chloride is sparingly soluble, most of the silver chloride solid would exist as solid.

Notice that the solid (AgCl) is NOT included in the Ksp expression. 

This is because the concentration of the solid ionic compound does not affect the equilibrium constant for ionic solutions. To elaborate, the concentration of solids are constant if temperature is not changed because solid’s density and molar mass are fixed. 

• Density = mass/volume.

• Concentration = moles/volume.

Since the molar mass of the ionic compound is fixed, density is essentially equal to concentration. As you may from junior science, the density of a solid is constant as the atoms are very closely held together by their chemical bonds, in this case, via ionic bonds. 

• Furthermore, if some of the solid (ionic compound) is dissociated into ions, its moles and volume will decrease such that its concentration will be constant.

• Vice versa, if ions react to precipitate the solid ionic compound, both the solid’s moles and volume will increase such that its concentration will also be constant.

Side note: The dissolution of sparingly soluble (‘insoluble’)  ionic compounds to form an equilibrium is an example of a heterogeneous equilibrium as there are different states of matter in the chemical reaction.

NOTE: Unlike other equilibrium constant formulas such as Kc, Ka, Kp, there is no denominator here for Ksp.

Effectively, the definition of Ksp is the equilibrium constant expression between a solid (i.e. ionic compound) and its ions. 

• From the example above: AgCl (s) <-> Ag+(aq) + Cl– (aq), the Ksp is equal to [Ag+] x [Cl–].

From the Ksp equation, a small Ksp value would mean the solid has a low solubility because the amount of ions dissociated in solution is small compared to the amount of solid

Anyways, similar to Ka and Kb, where we can determine extent of dissociation of acid and bases respectively, we can use Ksp to determine the extent of solubility of an ionic compound. That is, the higher the Ksp, the more soluble an ionic compound is. 

Side Note: As you can see from the Ksp expression, a higher Ksp value would mean that a higher concentration of ions are required to precipitate the corresponding ionic compound from solution.

Lastly, it is important to note that you CANNOT predict the relative solubility of ionic compounds using their Ksp values IF the ionic compounds being compared have different number of total ions released in solution per ionic compound. For example:

• For, BaCO3(s) <-> Ba2+ (aq) + CO3– (aq), the total moles of ions per one mole of dissolved ionic compound is 2 moles.

• For, Ag2CO3(s) <-> 2Ag+(aq) + CO3– (aq), the total moles of ions per one mole of dissolved ionic compound is 3 moles.

Since the total number of ions per ionic compound is different, you cannot use the Ksp value for BaCO3 and Ag2CO3 to determine the relative solubility of the two ionic compounds in water. 

• We need to calculate and compare the molar solubility of each ionic compound in order to determine which compound will precipitate first. The compound with the lower molar solubility, aka more ‘insoluble’, will precipitate first.

If the two compounds have the same total number of ions per molecule, then you can use Ksp to compare their relative solubilities. The compound with the higher the Ksp, will be more soluble due to higher molar solubility. This would mean the compound with the higher Ksp will precipitate last as higher concentration of ions are required to precipitate the compound as mentioned earlier.  

Let’s do an example, suppose you have a solution containing barium and silver ions. Then a fellow student added chromate ions into your solution. Will barium chromate precipitate first or silver chromate? You are given the solubility product constant for both barium chromate and silver chromate. Let’s have a look to see how we can determine which precipitate first!

Example of calculating molar solubility when total ions are DIFFERENT, given Ksp values.

As illustrated earlier, since the total number of ions when one mole of each ionic compound are dissolved are different, we cannot compare Ksp values. 

Therefore, we need to calculate the two ionic compound’s molar solubility separately then compare them.

Common Ion Effect

Suppose you have silver chloride dissolved in a beaker of water. Now, you decide to add some add sodium chloride into the AgCl solution. 

What you will find is that the the solubility of silver chloride will be lowered after sodium chloride have been added into the solution. But, why you may ask.

Well, suppose the Ksp of the dissolution of AgCl is x, i.e. some random value, where an equilibrium is established between AgCl and its silver and chloride ions.  

If you add sodium chloride into the silver chloride solution, you will increase the concentration of chloride ions. This would mean that the reaction quotient value will be greater than the Ksp value, x as the concentration of Cl- increased. 

As already mentioned in previous sections in this week’s notes, the reaction quotient value will move towards the Ksp value for equilibrium reactions when proceeding to reach equilibrium or re-establish.

In order for the reaction quotient value to decrease and re-establish equilibrium to due the increase chloride ion concentration offsetting equilibrium, the concentration of ions must decrease in the Ksp so that the Ksp value can be lowered and be equal to the Ksp constant.

This would mean that the concentration of chloride ions and silver ions will decrease as sodium chloride is added to the silver chloride solution, shifting equilibrium position to the left. 

This means that the solubility of silver chloride decreases because less chloride ions are dissociated into solution. This is known as the common-ion effect. 

This effect can be explained using Le Chatelier’s principle where the increase in the concentration of chloride ions due to the addition of NaCl will cause the equilibrium to shift its position such that it minimises the increase in [Cl– ions] by forming more silver chloride precipitate. 

This is because the chloride ion originating from silver chloride are already in equilibrium with AgCl and, as per Le Chatelier’s principle, addition of chloride ions from sodium chloride will cause the equilibrium position to shift to the left to minimise the disturbance. 

This would therefore lower the solubility of silver chloride as less AgCl is dissociated into its ions. 

Learning Objective #6 - Conduct an investigation to determine Keq of a chemical equilibrium system, for example:

- Keq of the Iron (III) thiocyanate equilibrium

This experiment is basically getting you to determine the equilibrium constant (Keq) of an equilibrium reaction. It is logical because we have studied many equilibrium constant formulas. 

Alright! Let’s see what we are doing here.

We need to calculate the equilibrium constant (Keq) for the following iron (III) thiocyanate equilibrium:

Fe3+ (aq) + SCN– (aq) <-> FeSCN2+ (aq) 

You would have seen this equation in Week 1’s notes. Just a recap, the Fe3+ ions will have a pale yellow colour, the SCN– ion is colourless and the FeSCN2+ ions have a crimson or blood red colour to them.

We want to calculate the equilibrium constant, so if we are going to write out the relevant formula it will be:

Keq = [FeSCN2+] / [Fe3+] [SCN–].

We want to calculate the concentrations of FeSCN2+, Fe3+ and SCN– at equilibrium in order to calculate the Keq of the iron (III) thiocyanate equilibrium reaction.

We can do this using the following procedure:

Step 1: Create five reference solutions made up of excess Fe3+ (from 0.2M Fe(NO3)3) and known concentrations of SCN–  (from 0.002M KSCN), making up a total volume of 10ml. 

Step 2: Calculate the concentration of SCN– and therefore FeSCN2+ ions after dilution by adding iron (III) nitrate solution. (using C1V1 = C2V2 dilution formula)

Step 3: Pour one reference solution into a cuvette (small rectangular tubular container) to place in the spectrophotometer to calculate absorbance. Rinse  cuvette thoroughly with water and dry it before measuring the absorbance of the next reference solution.

Step 4: Draw a calibration curve using the absorbance of each reference solution against the concentration of FeSCN2+ ions. 

Step 5: Create test solutions by adding a known quantity of Fe(NO3)3 solution and varying quantity of KSCN solution and water for a total of 10ml. Adding water helps ensure that the absorbance reading will be within the scale of your calibration curve so you avoid extrapolation! (This will help improve accuracy of results)

Step 6: Calculate the concentration of Fe3+ and SCN– ions in each test solution.

Step 7: Pour one test solution into a cuvette and into the spectrophotometer to calculate absorbance of test solution. Rinse the cuvette thoroughly with water and dry it before measuring the absorbance of the next test solution.

Step 8: Determine the concentration of FeSCN2+ for each test solution using the absorbance results and the calibration curve.

Step 9: Calculate the equilibrium constant for each of the test solution, average the Keq for each test solution to find the average Keq of the iron (III) thiocyanate solution and average deviation of the average Keq value. This is done by using the results obtained in Step 6 (INITIAL concentrations of Fe3+ and SCN–) and Step 8 (EQUILIBRIUM concentration of FeSCN2+) and the ICE table to compute the EQUILIBRIUM concentrations of Fe3+ and SCN– ions. 

NOTE: The initial concentration of FeSCN2+ is zero.

How to find average deviation:

Find the absolute value of the difference between your five 5 Keq values with the mean Keq value. You should have 5 different answers, one for each test solution.

Then, average these five absolute differences (numbers) to arrive to your average deviation for your average Keq value.

Potential Reference & Test Solutions Amounts

Preparing Reference Solutions’ (Example Quantities):

Reference solution #1: 8ml of iron (III) nitrate, 2ml KSCN

Reference solution #2: 7ml of iron (III) nitrate, 3ml of KSCN

Reference Solution #3: 6ml of iron (III) nitrate, 4ml of KSCN

Reference Solution #4: 5ml of iron (III) nitrate, 5ml of KSCN

Reference Solution #5: 4ml of iron (III) nitrate, 6ml of KSCN

Preparing Test Solution (Example Quantities):

Test Solution #1: 5ml of iron (III) nitrate, 1 ml of KSCN, 4 ml of water

Test Solution #2: 5ml of iron (III) nitrate, 2ml of KSCN, 3ml of water

Test Solution #3: 5ml of iron (III) nitrate, 3ml of KSCN, 2ml of water

Test Solution #4: 5ml of iron (III) nitrate, 4ml of KSCN, 1ml of water

Test Solution #5: 5ml of iron (III) nitrate, 5ml of KSCN

Creating the calibration curve for Step 4

Step 1: Plot your known FeSCN2+ concentration of your five reference solution across the x-axis. These concentrations can be computed via simple molar ratio between SCN– and FeSCN2+ as Fe3+ ions are in added excess when creating reference solution. So, SCN– is the limiting reagent. 

• These will help create an x-axis of a range of FeSCN2+ concentrations at equilibrium which you will need for step 8.

Step 2: Create a data plot for each reference solution by matching your calculated FeSCN2+ concentration with absorbance reading of your reference solution.

Step 3: Draw a line of best fit. This is a line that has equal data point on both side and each data point has roughly similar distance from the line of best fit. 

Finding the concentration of FeSCN2+ ions using absorbance readings of test solutions.

(Step 8)

For each test solution, you will get a different absorbance reading due to different concentration of FeSCN2+ ions. 

For each absorbance value that you get from the spectrophotometer machine, you can use the same calibration that you created in step 4 to obtain the corresponding FeSCN2+ concentration at equilibrium by reading across the y-axis until the best line of fit and then down towards the x-axis.

From here, you need to calculate the equilibrium concentration of SCN– ions and Fe3+ ions using the ICE table. This can be done using KNOWN INITIAL (diluted) CONCENTRATIONS of Fe3+, SCN– and FeSCN2+ when you made the reference solutions (step 2) as well as the known [FESCN2+] at EQUILIBRIUM from test solution using calibration curve (step 8).

NOTE: If your absorbance reading are too high, you should not extrapolate your line of best fit. The purple line in the diagram is example where you think you may need to extrapolate your line of best fit. However, It is bad to extrapolate as it reduces the accuracy of your Keq value for that test solution. This will then affect your average Keq for the overall iron (III) thiocyanate equilibrium reaction. This is why the dilution of solution in step 5 is important as it lowers the concentration of FeSCN2+ ions. Hence, your absorbance values will lie within the calibration curve created in step 4. In the event you get a reading such as the purple line, you need to make test solution, you may have made an error. OR, ignore the result if your other results are consistent (giving a similar Keq)

Week 3 Homework Set

Week 3 Homework Question 1 – Explain when it is appropriate to compare the relativity of ionic compounds using Ksp value and when it is not. 

Week 3 Homework Question 2 – Outline all the different types of equilibrium constants mentioned in this week’s notes and describe the scenario when you will use each one. 

Week 3 Homework Question 3 – Explain how the equilibrium position will be affected alongside the concentration of species for the Haber Process when the reaction quotient is greater, less and equal to the equilibrium constant. 

Week 3 Homework Question 4 – Suppose we have the reaction: Cl2 (g) <-> 2Cl(g) with a hypothetical equilibrium constant of 0.4. Calculate the concentration of Cl2 and Cl at equilibrium. Assume you initially have 1M of chlorine gas.

Week 3 Homework Question 5 – Suppose we have the following reaction: H2CO3 <-> H+ (aq) + HCO3– (aq) with a hypothetical equilibrium constant of 4.2 x 10-7. Calculate the concentration of each of the three species involved in the equilibrium reaction. Assume you initially have 0.1M of carbonic acid.

Week 3 Homework Question 6 – Suppose we have the following reaction: HF (aq) <-> H+ (aq) + F– (aq) with a hypothetical equilibrium constant of 7.2×10-7. Calculate the concentration of each of thee species involved in the equilibrium reaction. Assume you initially have 0.01M of HF.

Week 3 Homework Question 7 – Explain the effect of increasing and decreasing temperature on the equilibrium constant for the Haber Process. (Note: There are two scenarios here) 

Week 3 Homework Question 8 – Design an experiment to calculate the equilibrium constant for the iron (III) thiocyanate equilibrium. 

Week 3 Homework Question 9 – Suppose the current concentration of ammonia involved in the Haber Process is 2M. The temperature of the system is 700 degrees celsius. At equilibrium, 60% of the ammonia was found to remain. Calculate the equilibrium constant.

Week 3 Homework Question 10 – For the Haber Process, N2 + 3H2 <-> 2NH3. 

Draw a table and outline how the concentration of each species changes, direction which the equilibrium position will shift and the change in equilibrium constant (for forward reaction) if the following disturbances were made to the system:

• Increase in temperature

• Decrease in temperature

• Addition of nitrogen gas

• Addition of ammonia

• Removal of nitrogen gas

• Removal of ammonia

• Increasing volume

• Decreasing volume

Week 4 Curveball Question

Curveball Question 1 – Explain whether or not changing the concentration of species involved in an equilibrium reaction will alter the equilibrium constant value.

Curveball Question 2 – Explain whether the initial concentrations of species involved in an equilibrium will affect the equilibrium constant value.

Curveball Question 3 – Explain whether or not a catalyst will affect the equilibrium constant for an equilibrium reaction.

Curveball Question 4 – Determine the concentration of hydrogen gas at equilibrium for the chemical equilibrium, 2H2S(g) <-> 2H2(g) + S2(g) where Kc is equal to 1.7 x 10-7, temperature is 800 degrees celsius and the volume of the system is 0.500 litres . Additionally, there was 0.0125 moles of hydrogen sulfide.

Curveball Question 5 – Suppose you have the following reaction: O(l) + W(s) + O(l) <-> Y(g) + Z(g). Explain how would you decrease the concentration of Y. 

Curveball Question 6 – Suppose you have lead (II) chloride partially dissolved water. When you add salt into the solution, you find that there is a drop in the concentration of lead ions and solubility of lead (II) chloride. Name and describe this effect and explain how this effect can be accounted for using Le Chatelier’s Principle.

Solution to Week 3 Homework Questions

Solution to Question #1: 

It is only appropriate to compare two ionic compound’s solubility using their Ksp values provided that the compounds have the same total number of ions when dissociated in solutions. 

For example,

• when sodium chloride dissolves in water, NaCl(s) <-> Na+ (aq) + Cl– (aq), it releases two ions.

• when copper (II) chloride dissolves in water, CuCl2(s) <-> Cu2+ (aq) + 2Cl– (aq), it releases three ions.

Since these two compounds have different number of total ions it would NOT be appropriate to from their solubility using their Ksp value. In the case where two compounds have the same total ions per compound in solution, the compound with the higher Ksp value has greater solubility. 

Solution to Question #2:

All of the Keq will help determine the concentration of species at equilibrium. However, they differ depending on what information is given and/or purpose of the question

Kc – calculating the equilibrium constant for species when given their concentration

Kp – calculating the equilibrium constant for gases when given each species’ (partial) pressure

Ka – calculating the dissociation of acid constant, useful in determining strength of acid

Kb – calculating the dissociation of base constant, useful in determining strength of base.

Ksp – calculating the solubility product constant of solid dissociating into its ions, useful in determining molar solubility of solid

Solution to Question #3:

The reaction quotient (Q) is useful to help inform the direction at which the equilibrium position will shift to reach equilibrium.

If the reaction quotient (Q) is greater than the equilibrium constant for the chemical reaction then, to reach equilibrium, the reaction quotient value will move to match the equilibrium constant value. That is, it will decrease. This would mean that the product’s concentration will decrease (numerator) and the reactant’s species (denominator) will increase.

If the reaction quotient (Q) is less than the equilibrium constant for the chemical reaction then, to reach equilibrium, the reaction quotient value will move to match the equilibrium constant value. That is, it will increase. This would mean that the product’s concentration (numerator) will increase and the reactant’s species (denominator) will decrease. 

If the reaction quotient (Q) is equal to the equilibrium constant, there will be no changes in the species’ concentration that are participating in the equilibrium reaction. This is because the system has reached equilibrium and the equilibrium position will not shift as long as there is no disturbance applied to the system.

Solution to Question #4

Solution to Question 5

Explanation of assumption method:

The assumption method is ONLY valid if x is less than 5% than the initial concentration. In this case example, x is subtracting from initial concentration, 0.1M. 

To use the assumption method, we first assume that x is less than 5% of 0.1. Every time we make this assumption, it means that the value of x is small such that it is negligible. So, the denominator just becomes 0.1 in our example since 0.1 – x = 0.1, as x is so small it is negligible.

Following this, we perform the calculation to solve for x in the numerator. Notice that by using the assumption, we avoid using quadratic formula to solve. Instead, it’s just a simple square root to solve for x. This is why assumption helps us in simplifying the calculation process for x.

After we have calculated the value of x, we need to verify whether our 5% assumption rule is in fact valid. We do this by simply dividing the x value which we found by 0.1. 

Recall that we assumed that x is less than 5% than the value it is subtracting from, i.e. 0.1 in this case. If we do the assumption, we get that the value of x (i.e. 2.049 x 10-14) is 0.2049% of 0.1. 

Since 0.2049% is less than 5%, our assumption for x being negligible is correct. So, we are free to use x = 2.049 x 10-14 and substitute it into the ICE table to calculate the equilibrium concentrations of the species (reactant and products) in the equilibrium reaction. 

Assumption rule can be applied to weak acid and bases dissociation questions. Not for strong acid and strong bases. For HSC purposes, strong acid don’t have a K value (however it does higher chemistry courses), and so you only use ICE tables for weak acids and base dissociation questions. 

Strong acid and strong bases have the definition that the acid or base molecules completely dissociate into their ions in solution. So, it’s a one way arrow instead of two way, not an equilibrium reaction. No need for ICE table to find equilibrium concentration.

As you can see, the answers for the concentration of hydrogen ions and hydrogen carbonate ions is slightly different depending on which method you use. However, NESA permits you to use the assumption method as outlined in their sample paper for HSC Chemistry. Generally, I would only use the assumption method the the value that x is from subtracting from is small such as 0.1M or lower. Either way, remember to verify your assumption (less than 5%) as shown above.

Solution to Question #6

The ‘x’ value must be solved using Quadratic as the 5% assumption fails. 

x = 0.00235M after solving via quadratic. 

x = 0.00235 M = [HF] and [F-] at equilibrium from ICE table. Therefore, the [HF] and [F-] are both equal to 0.002 (to one sig. fig)

[HF] at equilibrium is 1 – x from ICE table = 1 – 0.00235 = 0.008 (to 1 sig fig.)

Solution to Question #7:

The forward reaction for the Haber Process is an exothermic equilibrium reaction. According to Le Chatelier’s Principle, when temperature of the system increases, the system will shift its equilibrium position to the left in favour of the reverse endothermic reaction. This is because the endothermic reaction will consume the excess heat added into the system, thus counteracting and minimising the disturbance (increased heat) to restore its equilibrium. This would mean the concentration of products (ammonia) will reduce and the concentrations of nitrogen and hydrogen (reactants) will increase. This will result in a decrease in the reaction’s  equilibrium constant value as Keq = [NH3]2 / [N2] [H2]3 or [products]/ [reactants]. 

When the system’s temperature decreases, the system position will shift in favour of the forward exothermic reaction to produce heat in order to counteract and minimise the decrease in temperature. Thus, the concentration of ammonia will increase whilst the concentrations of nitrogen and hydrogen will decrease. This will result in a decrease in the reaction’s equilibrium constant value. 

Solution to Question 8:

Please refer to the experimental procedure in the notes, the procedure is the answer. 

Solution to Question 9:

Solution to Question 10:

Solution to Week 3 Curveball Questions

Solution to Curveball Question #1

Temperature is the only factor that will affect the equilibrium constant value for a given chemical reaction. (You can elaborate on this by relating to the Rate Law and Arrhenius Equation covered in the week’s notes). Increasing or decreasing the concentration of species participating in the reaction will cause the equilibrium position to shift as per Le Chatelier’s principle to minimise the disturbance. This will only affect the reaction quotient. The ratio between the concentration of product and reactant will not be affected (constant) before and after the system’s equilibrium has been restored, hence the term equilibrium constant.

Solution to Curveball Question #2

Essentially the same answer for curveball question #1.

Temperature is the only factor that will affect the equilibrium constant value for a given chemical reaction. (You can elaborate on this by relating to the Rate Law and Arrhenius Equation covered in the week’s notes). Increasing or decreasing the initial concentration of species participating in the reaction will cause the equilibrium position to shift as per Le Chatelier’s principle to minimise the disturbance. This will only affect the reaction quotient. The ratio between the concentration of product and reactant will not be affected (constant) before and after the system’s equilibrium has been restored, hence the term equilibrium constant. 

Solution to Curveball Question #3

Catalysts only affect the equilibrium by lowering the activation energy required by reactants to interact and be converted into products (bond forming/breaking) and in equilibrium, it also lowers the activation energy required by products to interact and be converted into reactants. This means that catalysts speed up both the forward and reverse rates of reaction and reducing the time required by the species involved in the equilibrium reaction to reach equilibrium. This means that catalysts have no effect on the concentration of reactants and product at equilibrium.

Solution to Curveball Question #4:

Note that we are given the initial concentration of hydrogen sulfide and NOT the concentration of hydrogen and diatomic sulfur gas. 

This means that we write hydrogen sulfide on the left hand side of the ICE table, 2H2S(g) <-> 2H2(g) + S2(g). The order is important as it will affect the resulting value of Keq. 

So, if you write the chemical reaction and put it in ICE table in the order of 2H2(g) + S2(g) <-> 2H2S(g), you will get it wrong.

Solution to Curveball Question #5

The way to think about this question is to determine factors that will shift the position of the equilibrium reaction to the left. Note that the states on the left hand side are not gases. Hence, the molar ratio of gases on the left to the right side of the reaction is 0:2. Decreasing the volume or increasing pressure of the will cause the equilibrium position to shift to the left in favour of the side with the least moles of gas. This will decrease the concentration of Y (and Z).

Solution to Curveball Question #6

According to the common-ion effect, adding a solution to another solution that both consists of a common ion will cause the solubility of the substance containing the common ion to decrease in solubility.

In the question, since sodium chloride and lead chloride consists of the common chloride ion, as per the common-ion effect, the solubility of lead (II) chloride will decrease in solubility when sodium chloride is added into the solution. This is because the chloride ions from sodium chloride will react with the Pb2+ ions to form lead chloride. This lowers the solubility of lead (II) chloride and decrease the concentration of Pb2+ ions in solution.

The reaction between chloride ions with Pb2+ ions when sodium chloride is added lead (II) chloride to form lead (II) chloride can be explained using Le Chatelier’s principle.

As solid sodium chloride dissolves in the beaker consisting of water (and PbCl2), we can express the dissolution process as:

NaCl (s)  -> Na+ (aq) + Cl– (aq)  (removing H2O as spectator). [Equation 1]

PbCl2 (s)  <-> Pb2+ (aq) + 2Cl– (aq) (removing H2O as a spectator) [Equation 2]

The dissolution of sodium chloride in equation 1 would increase the concentration of chloride ion in the solution (containing chloride ions from the dissolution of lead chloride) which will shift equation 2 to the left, as per Le Chatelier’s Principle, to minimise the increase in the concentration chloride ion and increasing the concentration of lead (II) chloride precipitate. As solubility can be defined as the amount of ions that is dissolved in solution per mole of solute, the precipitation of the solute (lead (II) chloride) from solution reduces the amount of ions in solution and thus lowers the solubility of PbCl2.